|
一道有瑕疵的高考题
湖南省绥宁县第二中学 林安书
高考选择题往往以“小”、“精”、“巧”、“新”的姿态呈现在广大考生和高三一线教师的面前.纵观这几年高考题,其中不乏优秀之作,它们均遵循了命题的科学性、严谨性和合理性原则,这些题中绝大部分都体现了命题者的原创精神.是原创,就能体现出题目的“新”,是“新”就得经得住旧知的检验.下面笔者结合《几何画板》(最新版5.0)对2011年浙江省高考数学(理)第10题进行了研究分析,特指出其瑕疵,还请方家指正.
原题:(2011浙江理10)设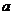 , , , , 为实数, 为实数,
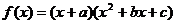 . .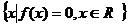 记集合S= 记集合S=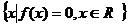 ,T= ,T=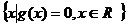 若 若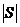 , , 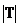 分别为集合元素S,T的元素个数,则下列结论不可能的是 分别为集合元素S,T的元素个数,则下列结论不可能的是
A.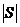 =1且 =1且 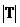 =0 B. =0 B.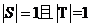
C.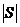 =2且 =2且  =2 D. =2 D. 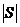 =2且 =2且  =3 =3
【解析】:此题为选择题,故可用特殊值法解答.
(ⅰ)当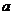 = =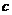 =0, =0,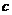 =2时, =2时, , ,此时 , ,此时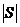 =1且 =1且  =0,见图(1); =0,见图(1);
(ⅱ)当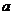 = =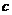 =2, =2,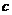 =0时, =0时,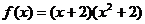 , , ,此时 ,此时
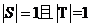 见图(2); 见图(2);
图(1) 图(2)
(ⅲ)当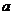 = =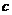 =4, =4, 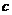 =-4时, =-4时, , ,
此时,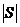 =2且 =2且 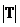 =2,见图(3); =2,见图(3);
(ⅳ)当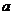 =3, =3,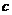 =-4, =-4,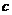 =4时, =4时, , ,
此时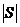 =2且 =2且  =3,见图(4). =3,见图(4).
图(3) 图(4)
通过以上分析,可知命题组给出的标准答案(D)有待商榷,因为A,B,C,D均有可能成立.其实此题考查的知识点不难,无非是函数零点概念和一元二次方程根的判别式的考查.难道正因为其难度不大我们的命题专家就放松了对此题的审察?这个问题我们姑且不去深究,我们现在只关心的是题目本身能给以后参加高考的学生带来多大的训练价值.结合优秀的教学软件《几何画板》,我们可以将此题对学生进行函数零点有关概念的复习.有兴趣的朋友不妨去研究一下:
︱S︱=0且︱T︱=0, ︱S︱=0且︱T︱=1,︱S︱=1且︱T︱=2,︱S︱=2且︱T︱=1,
︱S︱=1且︱T︱=3,︱S︱=3且︱T︱=1,︱S︱=3且︱T︱=2,︱S︱=3且︱T︱=0,
︱S︱=0且︱T︱=3,︱S︱=3且︱T︱=3
这些情况是否成立呢?我想,您是肯定能够得到收获的.
|